Ich bin Maschinenbauingenieur. Mein Elektrotechnikprofessor versuchte unsere Gilde ständig davon zu überzeugen, dass die Tage des Maschinenbaus gezählt sind und Mechanik durch Elektrotechnik ersetzt werden wird. Neben der fachlichen Ausbildung in seiner Disziplin liess er uns auch an seine Gedanken zu aktuellen Entwicklungen, der Menschheit und der Vergangenheit und Zukunft der Welt teilhaben. Dabei ist bei mir hängen geblieben, dass der Mensch Linearitäten schnell begreift. Exponentielle Zusammenhänge offenbaren sich unserer Spezies hingegen sehr schwer.
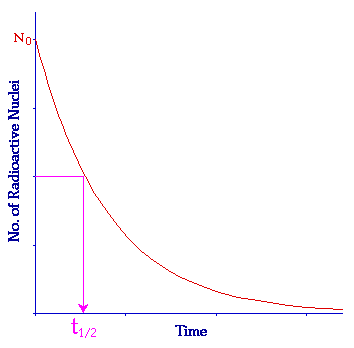
Die Politik hat in den letzten Jahren Wunder vollbracht; vielleicht nicht so sehr bei der Umsetzung und Realisierung von Programmen und Ideen als viel mehr bei der Prägung von Begriffen und die Übernahme dieser Begriffe in den allgemeinen Wortschatz. So begegnen mir diese Begriffe im Alltag und lassen meine Gedanken abschweifen, um mir der eigentlichen Bedeutung bewusst zu werden. Einer dieser Momente erlebte ich bei einem Vortrag, bei dem der Vortragende, ein medizinisch ausgebildeter Zeitgenosse, einen Begriff, den ich eher im naturwissenschaftlichen Umfeld erwarten würde: die Halbwertszeit.
Hier ging dieser Vertragende davon aus, dass nach Verstreichen dieser Zeitperiode das aktuell existierende Problem gelöst wäre. Das Fatale an der Halbwertszeit ist jedoch, dass es sich hierbei um einen bestimmten Zeitpunkt während eines exponentiellen Verlaufs handelt. Übertagen auf den Vortrag ist bei Erreichen dieses Zeitpunktes unglücklicherweise erst die Hälfte der Probleme gelöst. Warten wir so dann noch einmal so lange, werden wir hoffentlich in der Lage gewesen sein, eine weitere Hälfte der Hälfte an Problemen gelöst zu haben. Aber letztendlich werden wir unglücklicherweise auch in weit entfernter Zukunft bei dem hier gewählten Problemlösungsverlauf nicht in der Lage sein, alle Probleme zu unserer vollsten Zufriedenheit zu lösen.
Es ist somit sowohl bei der Nutzung der Atomenergie als auch bei der Lösung allzu menschlicher Probleme höchst unbefriedigend, bei einem exponentiellen Verlauf auf die Lösung eines gordischen Knotens zu hoffen.